无向图的建立和遍历(邻接矩阵法)
图的定义
图就是由一组顶点和一组能连接各个顶点间的边组成。
连通图:如果从任意一个顶点都存在一条路径到达另一个任意顶点,就称为连通图,一个非连通图由若干连通的部分组成,都称为极大连通子图。
无向图:即连接两个顶点的边是没有方向的。
图的表示
图在数据结构上可以用邻接表和邻接矩阵表示。我选择邻接矩阵,为啥?不为啥,就是因为我懒,邻接矩阵简单。
heap_sort
上面就是一个邻接矩阵,它代表了三个点,但没有边。默认顶点到它本身是没有边的,我在此邻接矩阵中用-1表示。此外1表示两顶点间有边,0则表示无。
图的遍历
一般我们说到图的遍历,就会提到深度优先搜索(DFS)和广度优先搜索(BFS)。
深度优先搜索
- 思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。显然,深度优先搜索是一个递归的过程。
广度优先搜索
- 思想:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2…的顶点。
举例
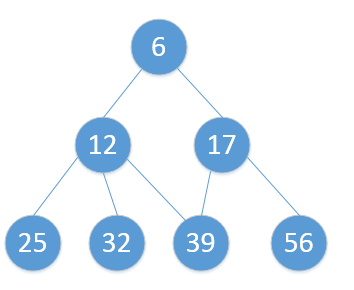
拿个例子说,如下的图:
graph
深度优先搜索遍历顺序为: 6,12,25,32,39,17,56
广度优先搜索遍历顺序为: 6,12,17,25,32,39,56
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111
| class Graph: def __init__(self,maps,edgeNum=0): self.map=maps self.nodeNum=len(maps) self.edgeNum=edgeNum def getNodeNum(self): return self.nodeNum def getEdgeNum(self): self.edgeNum=0 for i in range(self.nodeNum): for j in range(self.nodeNum-i): if self.map[i][j+i]==1: self.edgeNum+=1 return self.edgeNum def insertNode(self): for i in range(self.nodeNum): self.map[i].append(0) self.nodeNum+=1 ls=[0]*self.nodeNum self.map.append(ls) def deleteNode(self,x): for i in range(self.nodeNum): if self.map[i][x]==1: self.map[i][x]=0 self.edgeNum-=1 if self.map[x][i]==1: self.map[x][i]=0 self.edgeNum-=1 def addEdge(self,x,y): if x<y: if self.map[x][y]==0: self.map[x][y]=1 self.edgeNum+=1 else: if self.map[y][x]==0: self.map[y][x]=1 self.edgeNum+=1 def removeEdge(self,x,y): if self.map[x][y]==1: self.map[x][y]=0 self.edgeNum-=1 def BFSearch(self): visited=[0]*self.nodeNum queue=[] def bfs(self,i): print i if(visited[i]==0): visited[i]=1 for j in range(self.nodeNum): if(self.map[i][j]==1 and visited[j]==0): queue.append(j) for k in queue: if(visited[k]==0): bfs(self,k) del queue[:] for i in range(self.nodeNum): if(visited[i]==0): bfs(self,i) def DFSearch(self): visited=[0]*self.nodeNum def dfs(self,i): print i if(visited[i]==0): visited[i]=1 for j in range(self.nodeNum-i): if(self.map[i][j+i]==1 and visited[j+i]==0): dfs(self,j+i) for i in range(self.nodeNum): if(visited[i]==0): dfs(self,i) def test(): maps=[[-1,1,0], [0,-1,1], [0,0,-1]] G=Graph(maps) print G.getNodeNum() G.insertNode() G.insertNode() G.insertNode() print G.getNodeNum() print G.getEdgeNum() G.addEdge(1,4) print G.getEdgeNum() G.addEdge(4,1) G.addEdge(4,3) G.addEdge(2,5) G.addEdge(4,5) G.addEdge(3,5) print G.getEdgeNum() G.DFSearch() G.BFSearch() test()
|
Last updated:
© 2017 SakuraWood(Lee Sure)