八大排序算法（python描述）

冒泡排序

冒泡排序是最简单的排序？其实我并不觉得，只是在学算法的时候第一个接触的恰恰是冒泡排序。
什么，你说哪个是最简单的？这个仁者见仁吧。。。

  • 基本思想： 两两比较，然后决定是否交换

代码如下：

1
2
3
4
5
6
7
8
9
def bubble_sort(lists):
    length=len(lists)
    for i in range(0,length):
        for j in range(i+1,length):
            if(lists[i]>lists[j]):
                temp=lists[i]
                lists[i]=lists[j]
                lists[j]=temp
    return lists

再来分析一波时间复杂度，嗯，这个时间复杂度应该为：
0+1+2+3+······+n-1
即n的累加，等于n*(n-1)/2。时间复杂度为O(n²)

直接选择排序

好吧，我只是单纯认为这个是最简单的排序。
设想一下吧，假如给你一套扑克牌，从A到K一共13张乱序的牌，你会怎么把它排好序？
我想你应该是这样，先把A选出来，再把2选出来，以此类推，最后把K选出来。
你难道不是这样？别告诉我你是按照冒泡那样排的，如果你真那样做的，我服你=。=

  • 基本思想： 第1趟，在待排序记录r[1] ~ r[n]中选出最小的记录，将它与r[1]交换；
    第2趟，在待排序记录r[2] ~ r[n]中选出最小的记录，将它与r[2]交换；
    以此类推，第i趟在待排序记录r[i] ~ r[n]中选出最小的记录，将它与r[i]交换，使有序序列不断增长直到全部排序完毕。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
def select_sort(lists):
    length=len(lists)
    index =0 
    while(index<length):
        min=index
        for i in range(index,length):
            if(lists[i]<lists[min]):
                min=i
        temp=lists[index]
        lists[index]=lists[min]
        lists[min]=temp
        index+=1
    return lists

时间复杂度：
这看上去和冒泡排序是一样的，所以复杂度也是O(n²)

插入排序

现在要看得是插入排序，怎么个插入法？

  • 基本思想： 通俗点讲，就是在已经排好序的数组中，插入将要插入的数，使得这个数组依然有序。

Wtf？我为什么要插入？数组就在那而已嘛。。。百科上有张图可以让你理解一下:

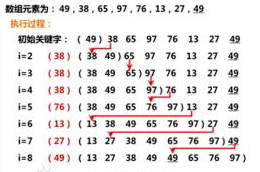
insert_sort
insert_sort

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
def insert_sort(lists):
    length=len(lists)
    for i in range(1,length):
        j=i-1
        key=lists[i]
        while j>=0 and lists[j]>key:
            # while j>=0:
                # if(lists[j]>key): 注意了，有些哥们儿是这样写的，但其实这样浪费了比较操作，显得比冒泡还慢
                # 其实终止条件是遇上前面第一个小的就停止循环，因为之前的都是排好序的
            lists[j+1]=lists[j]
            lists[j]=key
            j-=1
    return lists

时间复杂度：
这东西一看，时间复杂度也是O(n²),在最坏的情况下，和冒泡是一样的，但是万一没那么坑爹(不需要每趟都要和之前的所有元素都比较)，
它就比冒泡要快一点。

希尔排序

希尔排序是一个叫希尔的人发明的，它是直接插入排序的进化版本。

  • 基本思想：对数组按增量分组，组内再进行直接插入排序

什么增量分组？还是直接从百科上借张图来可能好理解一点：

insert_sort
insert_sort

所以，这个增量怎么确定？其实关于这个增量，都够人研究的了，有专门的论文讨论哪个增量序列好。
我们在这里假设起始增量为数组长度的一半，后面则除以2取整，直到1结束。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
def shell_sort(lists):
    length=len(lists)
    step=length/2
    while step>=1:                      # 比起直接选择排序，就多了这一层
        for i in range(step,length):
            j=i-step
            key=lists[i]
            while j>=0 and lists[j]>key:
                lists[j+step]=lists[j]
                lists[j]=key
                j-=step
        step/=2
    return lists

时间复杂度:
“喂，这看上去多了一层while循环了，还搞个毛啊。。。”
没错，这确实是多了一层while循环，但是你想，你不用每趟都像增量为1的直接插入排序那样交换那么多次啊。。。
本质上讲，希尔排序算法是直接插入排序算法的一种改进，减少了其复制的次数，速度要快很多。 原因是，当n值很大时数据项每一趟排序需要移动的个数很少，但数据项的距离很长。当n值减小时每一趟需要移动的数据增多，此时已经接近于它们排序后的最终位置。 正是这两种情况的结合才使希尔排序效率比插入排序高很多。

你把代码复制过去，自己跑一跑，会发现到后面，最里层的while循环会很快跳出，甚至都进不去，实际的数据交换操作是比普通的直接插入排序要少很多的。希尔排序的时间复杂度取决于增量序列的选取，在本例中这个增量序列条件下（此增量序列叫希尔增量），希尔排序的时间复杂度为O(n²)。当然还有更好的增量序列，不过，希尔排序时间复杂度的下界是nlog2n。
“什么，不都三层循环了么，你逗我呢？”
“。。。”
呃，你可以看下代码里的增量序列，每次都除以2。。。不知道你们之前学数学有没有接触过1+2+4+8+······+m =。=
而这个m就是你设置的起始增量。你看，其实最外层while的次数就是m以2为底的对数log2(m)。
“那岂不是O(n²logn)?”
“好吧，我承认这比较难。”
这个确实困扰到我了，上面说了，希尔排序算法的性能与所选取的增量序列有很大关系。只对特定的待排序记录序列，可以准确地估算关键词的比较次数和对象移动次数。不知道有谁可以分析出在有增量序列的情况下，while循环内的操作时间复杂度如何计算？内层的while的break触发是否与增量有关系？

快速排序

好了，终于到了大名鼎鼎的快排了。顾名思义，它就是快。

  • 基本思想： 通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，
    然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

举例说明一下吧，这个可能不是太好理解。假设要排序的序列为

16,7,3,20,17,8,19,54,12

游戏规则：

  • 首先，取第一个数作为key，同时你有两个指针，一个左指针，一个右指针，右指针从最右边往左扫描，左指针则从最左往右扫描，从右指针开始；
  • 右指针往左扫描过程中，遇上比key大的，则跳过，右指针左移。遇上比key小的，则把右指针的数换到左指针所在的位置，然后，比较操作切换成左指针；
  • 左指针往右扫描过程中，遇上比key小的，则跳过，左指针右移。遇上比key大的，则把左指针的数换到右指针所在的位置，然后，比较操作切换成右指针；
  • 左指针和右指针下标相遇，停止，将key放到该位置；
    估计还是不明白，好吧，开始跑:

key: 16 16,7,3,20,17,8,19,54,12 第一个数是16吧？右指针开始了，遇到12，根据规则，12比16小，直接换到左边，切换操作到左指针；

key: 16 12,7,3,20,17,8,19,54,12 好，这下从左边看7，7比16小，根据规则，不用换，但左指针右移；

key: 16 12,7,3,20,17,8,19,54,12 继续看3，3还是比16小，根据规则，不用换，左指针左移；

key: 16 12,7,3,20,17,8,19,54,12 继续看20，20比16大，直接换到右边，切换操作到右指针；

key: 16 12,7,3,20,17,8,19,54,20 看20，20比16大，根据规则，不用换，右指针左移；

key: 16 12,7,3,20,17,8,19,54,20 看54，54比16大，不用换，右指针左移；

key: 16 12,7,3,20,17,8,19,54,20 19也比16大，继续左移；

key: 16 12,7,3,20,17,8,19,54,20 8比16小，根据规则，直接换到左边，切换操作到左指针；

key: 16 12,7,3,8,17,8,19,54,20 再来看左边，8比16小，根据规则，不用换，左指针右移；

key: 16 12,7,3,8,17,8,19,54,20 17比16大，直接换，切换操作到右指针；

key: 16 12,7,3,8,17,17,19,54,20 再来看右边，17比16大，不用换，右指针左移，额(⊙o⊙)…这么一换，和左指针相遇了哦

key: 16 12,7,3,8,17,17,19,54,20 终于相遇了，那就根据规则把key：16 放到这吧。

一趟之后的最终结果：
key: 16 12,7,3,8,16,17,19,54,20

这样子走了一趟后，你可以看到key：16把整个数组分成了两部分。知道接下来干嘛了吧？没错，就是递归，对这两个子区间分别都这样再跑，直到分解的部分长度为1。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def quick_sort(lists):
    low= 0
    high=len(lists)-1
    def quick_sort_helper(lists,low,high):
        left=low
        right=high
        key=lists[low]    # 选择第一个元素作为key
        while(left<right):
            while(list[right]>=key and left<right):
                right-=1
            lists[left]=lists[right]
            while(list[left]<=key and left<right):
                left+=1
            lists[right]=lists[left]
        lists[left]=key
        if(low<left):
            quick_sort_helper(lists,low,left-1)
        if(high>left):
            quick_sort_helper(lists,left+1,high)
    quick_sort_helper(lists,low,high)
    return lists

分析一波时间复杂度，假设每次划分子区间都平均，为n/2，那意味着快排结束的越早，时间复杂度为O(nlogn)。当然最坏情况自然是O(n²)了（数据恰好是倒序就是这种情况，你可以试试）。

堆排序

堆排序是啥？堆排序是针对具有堆结构的数据进行的排序。

二叉堆的定义

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。

最大堆示例图：

heap_sort
heap_sort

  • 基本思想：堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1…n]中选择最大记录，需比较n-1次，然后从R[1…n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。

  • 步骤：

  1. 建堆
  2. 调整堆
  3. 排序
    排序的时候，根据最大堆或最小堆的定义，堆顶元素永远最大或最小，与堆顶元素交换，并实时调整堆，最后可使整个数组有序。事实上，排序的过程也是一个不断在调整堆的过程。

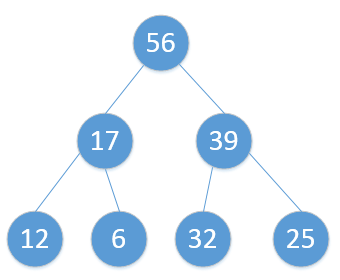
可能有点晦涩难懂，还是上图吧，假设需要排序的数组为：[12,56,32,17,6,39,25]，要构造的堆是最大堆。

  1. 建堆：
    原始是这样的：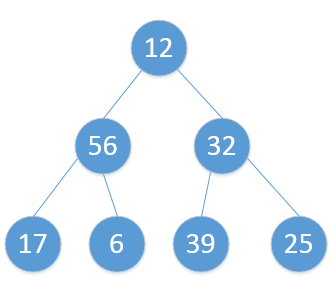

    heap_sort
    heap_sort

  2. 调整堆：
    从倒数第一个非叶节点开始，

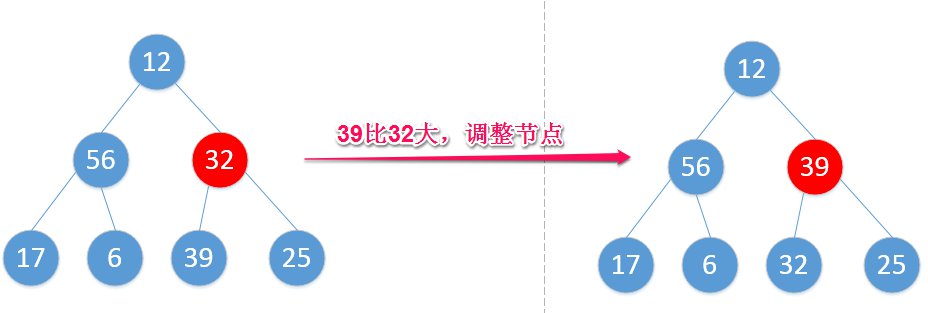
heap_sort
heap_sort

倒数第二个，56比10和6都大，此左子树符合最大堆定义，不用动：

heap_sort
heap_sort

12比56和39小，选较大的，调整节点：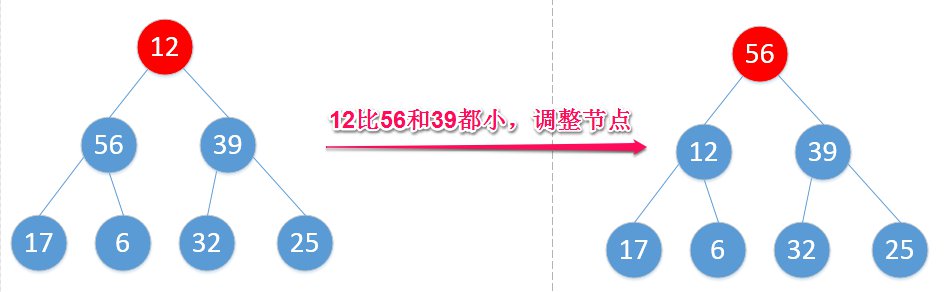

heap_sort
heap_sort

你该不会以为这样就完了吧？可以看到把56换到根节点后，12这个节点又在搞事，还需调整：

heap_sort
heap_sort

调整完毕，构造了一个最大堆：

heap_sort
heap_sort

  1. 排序：
    记住，堆排序的过程，不仅仅是单纯地和堆顶元素进行交换，每交换之后都要检查一遍，对整个堆进行调整。

那么继续，25比56小，直接换，请注意，你已经把最大的元素拿下来了，所以，56就被此最大堆“开除”了。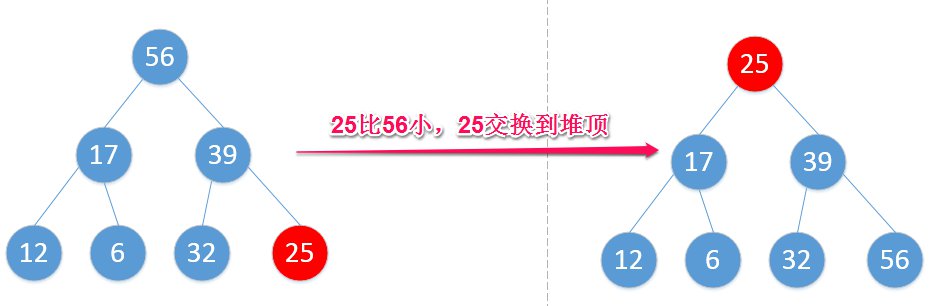

heap_sort
heap_sort

然后你发现，这一换不得了，堆顶不符合最大堆定义了，需要调整堆: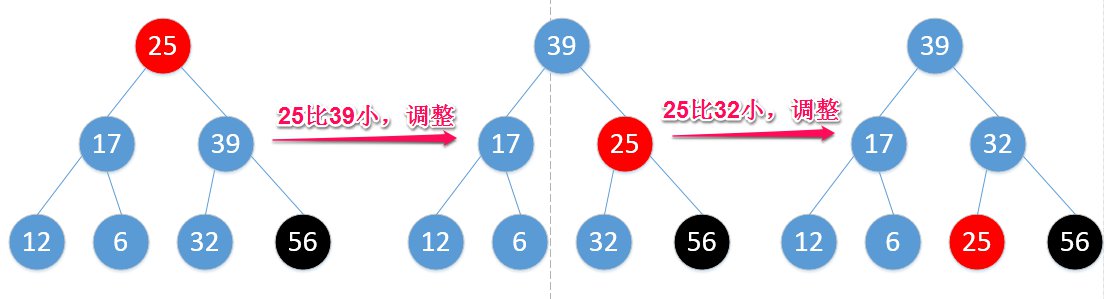

heap_sort
heap_sort

这么一调，除了56外，重新符合了最大堆的定义，那么再从25开始，继续替换堆顶元素：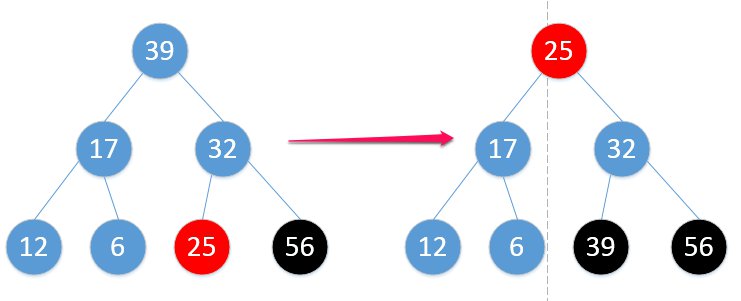

heap_sort
heap_sort

这样，39被“开除”，但此时又不符合最大堆定义，又得调整：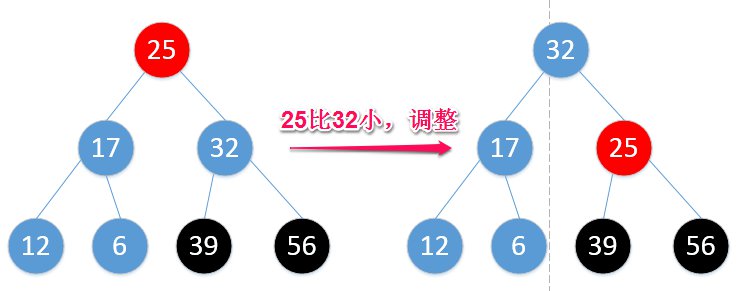

heap_sort
heap_sort

之后的操作，我用图来演示，估计你也能看得懂了：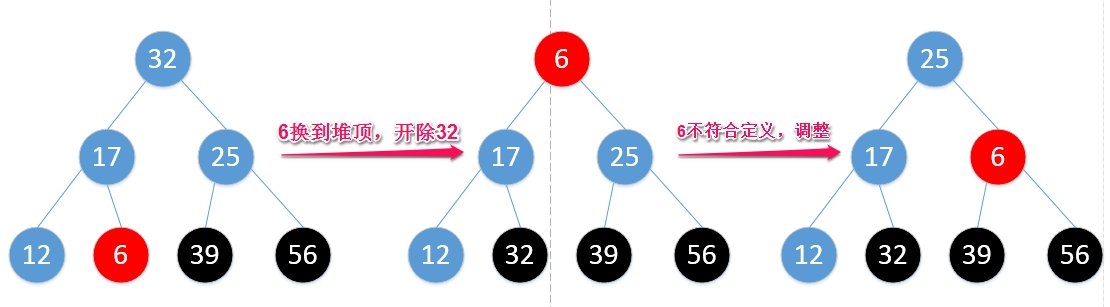

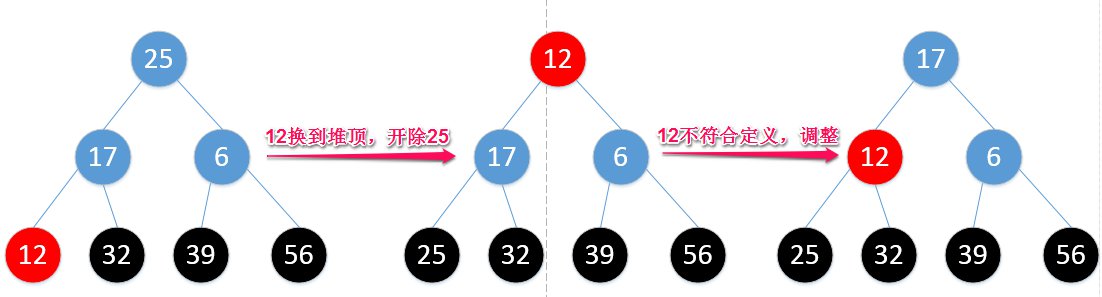
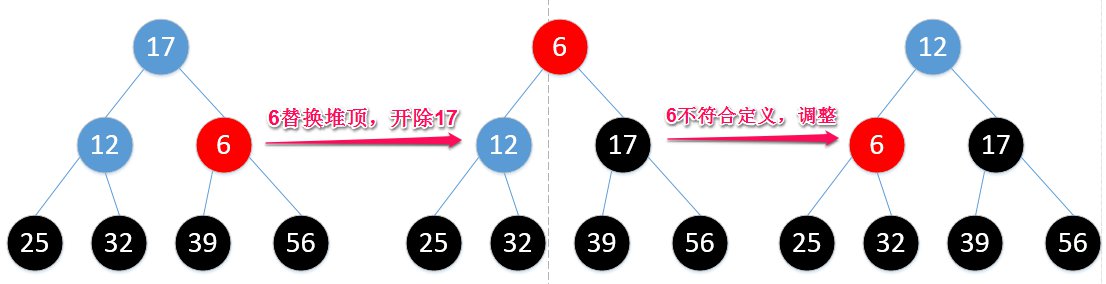
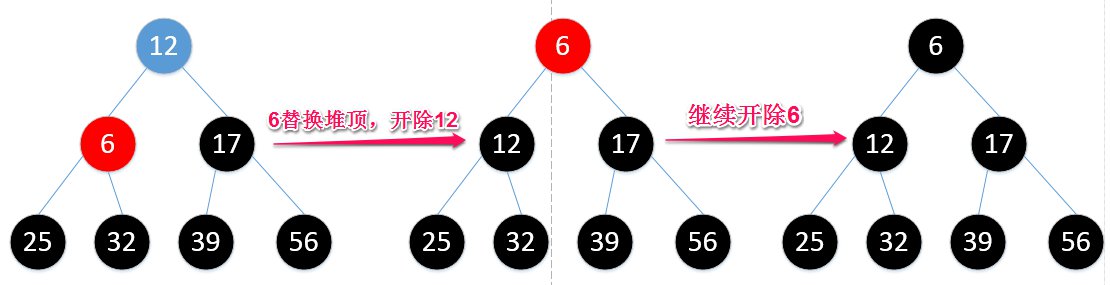
heap_sort
heap_sort

heap_sort
heap_sort

heap_sort
heap_sort

heap_sort
heap_sort

所以，最终结果就是：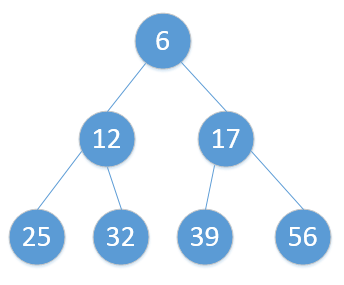

heap_sort
heap_sort

其实不是“开除”，而是把元素一个一个选出来，有些人直接看定义看不明白，看图总知道怎么选的了吧？我知道有疑问，估计是，为什么在创建堆的时候，调整堆的策略跟后面堆排序时调整堆的策略看上去有点不一样？

有一点，要搞明白，在创建堆之后，我的目的是要这整个堆调整成一个最大堆；而后面堆排序，我是要利用最大堆的性质，不断地把堆顶元素选出来，同时把未选的剩下元素调整成最大堆。

什么？这两步调整堆的策略不一样？其实是一样的，调整堆，其实就在递归纠正整个树的过程，你只需要关心以某个节点为根节点的树及其子树是否满足最大堆而已，是就不调整，不是就调整。

  • 创建堆的时候，是从第一个非叶节点开始，倒序一直调整到根节点，当然每一步调整都用到递归；
  • 堆排序的时候，调整的对象一直是根节点，当然每一步调整也都用到递归；

具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def heap_sort(lists):
    length=len(lists)
    def create_heap(lists,length):
        for i in range(0,length/2)[::-1]: #创建堆调整的时候，是从非叶节点开始的哦！！！
            adjust_heap(lists,i,length)
    def adjust_heap(lists,i,length):
        lchild = i*2+1
        rchild=i*2+2
        max=i
        if(lchild<length and lists[max]<lists[lchild]):
            max = lchild
        if(rchild<length and lists[max]<lists[rchild]):
            max = rchild
        if max!=i:
            lists[i],lists[max]=lists[max],lists[i]
            adjust_heap(lists,max,length)
    def heap_sort_helper(lists):
        for i in range(0,length)[::-1]:
            lists[0],lists[i]=lists[i],lists[0]
            adjust_heap(lists,0,i)          # 这一步，就是不断开除，不断调整节点的意思
    create_heap(lists,length
    heap_sort_helper(lists)
    return lists

最后，还是要分析一波时间复杂度，
先是建堆，这是一个从非叶节点开始调整的过程，假设树的高度为K（编号1到k层），那总共的元素，至多为2^k-1。从k-1层开始调整，第k-1层的元素数量是2^(k-2)，这个应该没有疑问，在这一层上的元素，所需调整的次数为1；而每往上一层，次数就要加1。所以，总共时间可以归结为：
S= 2^(k-2)1+ 2^(k-3)2+ 2^(k-4)3+……+1(k-1)

这种数列求和，就用错位相减法，先两边都乘以2：

2S= 2^(k-1)+2^(k-2)2+ 2^(k-3)3+……+2*(k-1)

再减去原来的式子，刚好得到：
S= 2^(k-1)+2^(k-2)+……+1-k

除去最后一项，是一个等比数列求和，根据求和公式，可以得到：S= 2^k-1-k
如果节点数量为n，那么n与k的关系就是n=2^k-1,k=log(n+1),所以，S=n-log(n+1),
∴建立最大堆的时间复杂度为O(n)。

明白了这个，那么排序的时间复杂度，应该也好计算。因为交换之后始终调整的是根节点，由上可知，根节点需要调整的次数是k-1，而且你要知道，每一步交换还“开除”了一个元素，当然，我们也不用算那么精准了，直接
S= n(k-1)=n(log(n+1)-1)
∴排序的时间复杂度为O(nlogn)。

归并排序

  • 思想：建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

  • 过程： 比较a[i]和b[j]的大小，若a[i]≤b[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素b[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

看这些定义，总是没那么形象，所以还是按照快排那样子，一步一步演示一下吧，继续拿上边的数组,
[12,56,32,17,6,39,25]

[12 56 32 17 6 39 25] 初始数组

[[12 56 32][17 6 39 25]] 分而治之，分成两部分，一部分[12 56 32]，一部分[17 6 39 25]

[[[12][56 32]][17 6 39 25]] 先只关心左边（强调一下，你当然可以同时操作右边，我只想说在串行操作下，算法是怎么跑的），对[12 56 32]继续划分，12被划分出来了，在只有一个元素的子部分，当然也就排好序了

[[[12][[56][32]]][17 6 39 25]] 只要还没有划分到只有一个元素，就继续划分

[[[12][32 56]][17 6 39 25]] 合并56和32，并排好序

[[12 32 56][17 6 39 25]] 合并[12]跟[32 56]，并排好序

[[12 32 56][[17 6] [39 25]]] 再来看刚才右边的部分，和左边一样，划分

[[12 32 56][[[17] [6]] [39 25]] 划分

[[12 32 56][[6 17] [39 25]]] 合并17和6，并排好序

[[12 32 56][[6 17] [[39] [25]]]] 划分

[[12 32 56][[6 17] [25 39]]] 合并39合25，并排好序

[[12 32 56][6 17 25 39]] 合并[6 17]和[25 39]，并排好序

[6 12 17 25 32 39 56] 合并[12 32 56]和[6 17 25 39]，并排好序

这样走下来，整个数组就排完序了。

乍一看，貌似还挺费劲的，划分然后又合并，折不折腾。。。
好吧，我先不上代码，来分析一下它的时间复杂度。可以看出，只要是划分了多少次，就要合并多少次。划分的次数不用看，当然是n了，有多少个就要分到底嘛=。=但是你这样二分法下来，二分了多少次，才确保全部子区间都划分成了只包含一个元素？logn。很显然啊，如果你看了前面几种排序，这应该是很简单的，2^k=n,k=logn。

时间复杂度为O(nlogn)。嗯，毫无疑问。可能有些疑问说你咋知道{12 32 56}和{6 17 25 39}合并排序的时候，比较次数就是7，而不是3*4=12？拜托，这俩子区间本身已经排好序了好不好？根据上面的过程描述，一路向右比较有疑问？那我直接上代码，自己跑跑便知：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def merge_sort(lists):
    def merge(left, right):
        i, j = 0, 0
        result = []
        while i < len(left) and j < len(right):
            if left[i] <= right[j]:
                result.append(left[i])
                i += 1
            else:
                result.append(right[j])
                j += 1
        result += left[i:]
        result += right[j:]
        return result
    if len(lists) <= 1:
        return lists
    num = len(lists) / 2
    left = merge_sort(lists[:num])
    right = merge_sort(lists[num:])
    return merge(left, right)

基数排序

其实，八大排序（传统版本，不包含优化）里速度能够跟快排相比（其实归并就跟快排不多快了）甚至超过快排的就是基排了。它相当的快，在我写的这些python排序程序里，它几乎每次都比快排要快，在数据量大的情况下，甚至比快排快一倍，后面我会贴图看看这些排序算法的运行时间。

  • 思想：基排的思想非常简单，它不像其他算法那样，都是基于直接的数值比较，它是基于数字在不同位数上的排序。
    思想是分配k个桶，编号0到k-1,从数值第0位开始按照桶编号对号入座（相当于在排序），以此类推直到最高位排序完毕。

举个例子吧，这次来个稍长一点的，[4,2,5,54,23,24,11,3234,3432,56,21,33,663,22,341,52]。

一般我们表示的是10进制数，假设我们给十进制数分配10个桶，编号0~9。

先来排个位数的，对号入座：

0

1 11,21,341,

2 2,3432,22,52,

3 23,33,663,

4 4,54,24,3234,

5 5,

6 56,

7

8

9

排完个位数之后，数组变为：[11,21,341,2,3432,22,52,23,33,663,4,54,24,3234,5,56]

接着是十位数上的排序，继续对号入座：

0 2,4,5,

1 11,

2 21,22,23,24,

3 3432,33,3234,

4 341,

5 52,54,56,

6 663

7

8

9

排完十位数之后，数组变为：[2,4,5,11,21,22,23,24,3432,33,3234,341,52,54,56,663]

接着百位数的：

0 2,4,5,11,21,22,23,24,33,52,54,56,

1

2 3234,

3 341,

4 3432,

5

6 663,

7

8

9

排完百位数之后，数组变为：[2,4,5,11,21,22,23,24,33,52,54,56,3234,341,3432,663]

接着千位数的：

0 2,4,5,11,21,22,23,24,33,52,54,56,341,663

1

2

3 3234,3432

4

5

6

7

8

9

得到结果：[2,4,5,11,21,22,23,24,33,52,54,56,341,663,3234,3432]

基数排序一看，就跟其他排序不一样，它属于“分配式”排序，根据数组元素数值上的部分信息在当前阶段分配到有序的桶里，再通过不同阶段的分配后使数组有序。

让我们分析一下它的时间复杂度，假设有n个元素，那么每个阶段分配到桶里时间就是n。那究竟跑了多少趟？这个显然与数组中的最大数值的位数有关。假设为k，那么就是kn。当然还有一个时间是收集时间，从桶里面把元素拿出来再组成一个一维数组，这个又与桶的数量有关，假设桶的数量为d,那么就是kd。所以时间复杂度为：O(k*(n+d))。

哎哟，这么一看，这基排还挺不错的，貌似比之前的都要强啊。但是基排也有缺点，就是空间开销比较大，你看它申请的这个桶数组还是二维的，不是一维的，除此之外还有一个额外的数组用来收集。空间复杂度为O(kd+n)。

直接上程序吧：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import math
def radix_sort(lists,radix=2):
    bits=int(math.ceil(math.log(max(lists),radix)))
    bucket=[[]for i in range(radix)]
    index=0
    while index<bits:
        for i in lists:
            bucket[i>>index&0x1].append(i)
        del lists[:]
        for j in bucket:
            lists+=j
            del j[:]
        index+=1
    return lists

后来我分析了一下，我这个基排为什么会快一些，是因为我只分配了两个桶，即0和1，我把所有数都当做二进制数的方式进行处理，这本来也是计算机的处理方式。然后按照移位处理，便可获取到位数上的值（0或1）进行对号入座。

PK

写了这么些排序函数，还是来PK一下吧：

无序数组（随机，长度50）：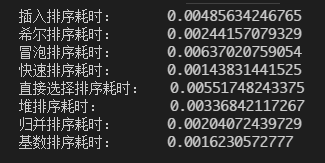

sort_pk
sort_pk

无序数组（随机，长度200）：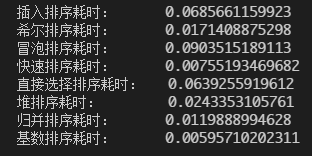

sort_pk
sort_pk

无序数组（随机，长度1000）：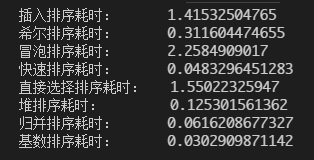

sort_pk
sort_pk

无序数组（随机，长度5000）：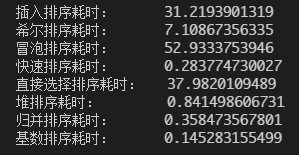

sort_pk
sort_pk

当然单位都是秒，可以看到，数组数量都还很少的时候，大家都差不多；当数量变大的时候，可以看到快排和基排都是最快的两个（我承认在此例中，基排简直逆天）；到最后，长度达到5000，我想你明白了O(n²)和O(nlogn)的差距了=。=