红黑树
- 红黑树(英语:Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。它是在1972年由鲁道夫·贝尔发明的,他称之为”对称二叉B树”,它现代的名字是在Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文中获得的。它是复杂的,但它的操作有着良好的最坏情况运行时间,并且在实践中是高效的:它可以在O(logn)时间内做查找,插入和删除,这里的n是树中元素的数目。
维基百科上的定义就这么说了。好像你看了之后也不知道它究竟是啥。因为红黑树本身是非常绅士(hentai)的数据结构。
二叉查找树
“自平衡二叉查找树?什么是平衡树?什么是二叉查找树?”
不得不说这由红黑树引发的关于Data Structure知识匮乏的一系列惨案。。。
回顾一下二叉查找树吧(基础好的同学可以略过直接跳往红黑树)。它满足以下性质:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
如何构造一颗二叉查找树?
首先一颗BST要包含插入、删除和查找等操作。
先定义一个节点:
初始化一棵树:
|
|
此时,根节点为空,大小为0,还没开始插入节点。
所以,插入考虑两种情况:
- 插入的是根节点
- 插入的不是根节点
插入根节点不用多说,但插入子节点有讲究,根据二叉查找树的定义,具体看代码:
|
|
插入了之后,就可以查找节点了,查找相当简单,多亏了这是二叉排序树,你只需要从金字塔顶端往下走就行,遇上小的往左,遇上大的往右,直到碰到和自己一样的:
|
|
呵呵,挺好的,貌似差不多了,,,不过还有删除呢。
删除这个操作,是二叉树里最烦的操作了。它涉及到各种情况,虽然写法不一,但思路都是一样,无外乎包含这四种情况:
- 被删节点是叶节点(不够准确,其实是既无左子树又无右子树)
- 被删节点有左子树但没有右子树
- 被删节点有右子树但没有左子树
- 被删节点左右子树都有
什么?还有被删节点是根节点?嗯,确实,它可以看做是1的一种特殊情况,它本身没有子节点,同时没有父节点。
首先理解一下前驱和后继的含义。
节点key的前驱,就是中序遍历时,比key小的所有节点中最大的那个节点。
节点key的后继,就是中序遍历时,比key大的所有节点中最小的那个节点。
所以,根据定义,被删节点用前驱或者后继替代都是合法的。
针对这四种情况,我列几张图,说明一下:
- 既无左子树又无右子树
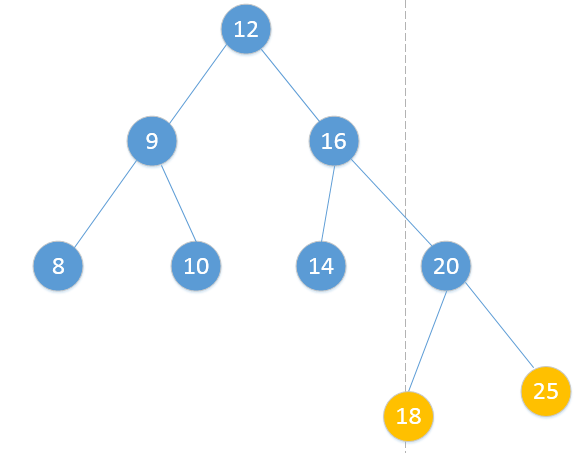
这俩节点都是属于这种情况,应该直接删掉。
- 有左子树但没有右子树
- 先解释一下,可以有两种做法,可以用左孩子节点替换,也可以用前驱节点替换,反正都符合二叉排序树的性质,我这里采用前驱节点替换:
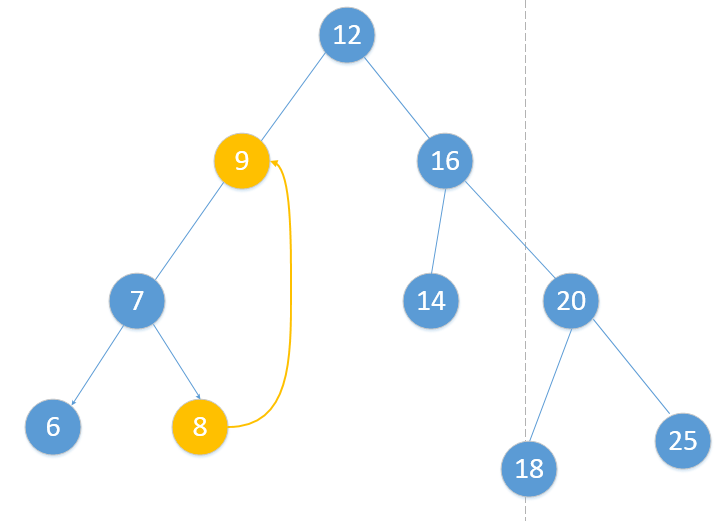
- 有右子树但没有左子树
- 同理地,可以有两种做法,可以用右孩子直接替换,也可以用后继节点替换,我这里采用了右孩子直接替换:
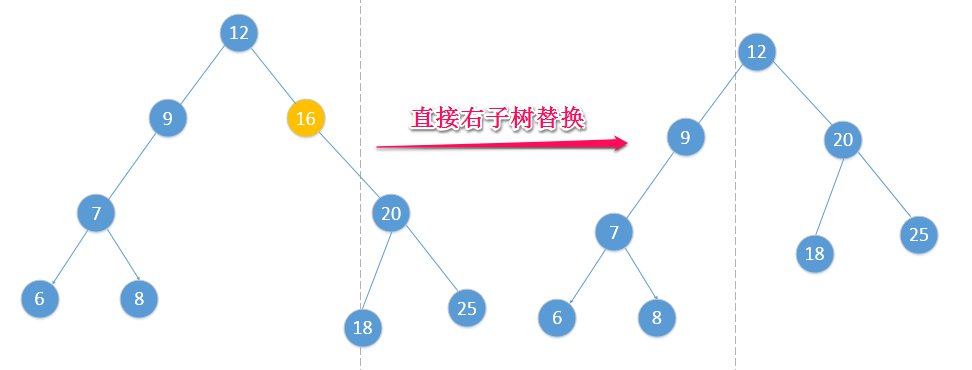
- 既有左子树又有右子树
- 同样地,可以有两种做法,可以用前驱节点替换,也可以用后继节点替换,这里采用后继节点替换:
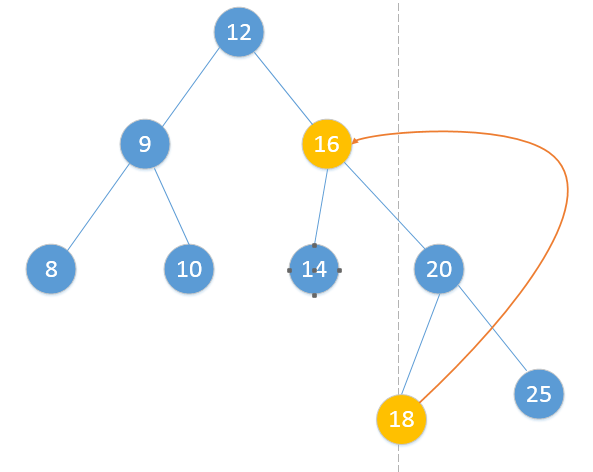
代码如下:
大致思路就是这样,二叉排序树就这样介绍完了。
来分析一波时间复杂度,按照二叉排序树的性质,只要是中序遍历,那肯定会生成一个有序序列。因为时间复杂度只与二叉树的深度有关,如果刚好这棵树的深度和节点数量一样(起始就是升序插入),那和顺序查找(时间复杂度O(n))没有区别=。=,这就杯具了。但乐观点讲,假入这个二叉排序树初始化的特别巧妙,恰好最后变成了一颗完全二叉树,岂不妙哉(时间复杂度O(logn))?
该如何确保它变成这样呢?所以有了平衡的概念,看来前人为了方便查找可谓是煞费苦心。
平衡二叉树
平衡二叉树是优化后的二叉排序树,在这里,平衡指所有叶子的深度趋于平衡,更广义的是指在树上所有可能查找的均摊复杂度偏低。
还是举个例子吧。
AVL树
AVL树,毫无疑问,典型中的典型。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(logn)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
“Wtf?平衡因子?树旋转?什么玩意儿?”
这么说吧,树旋转操作是把一颗普通排序树变为平衡树的核心操作,而这个操作要根据平衡因子来判断。这就跟节点删除一样,考虑的情况多,而且更加复杂。不过先不用急,慢慢来:
我们先来看张图:
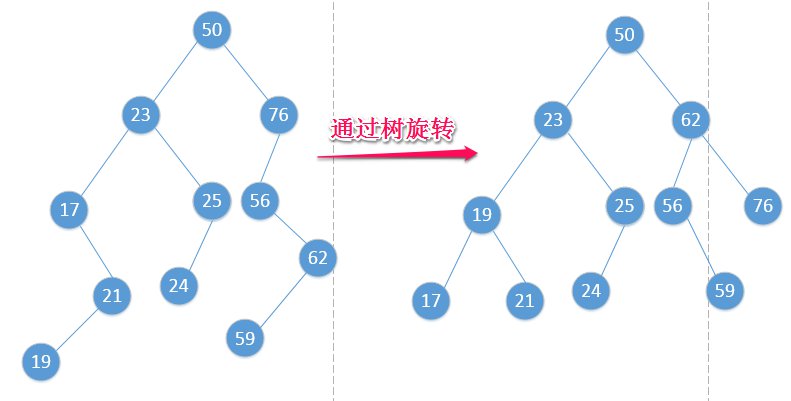
通过上面操作,树趋于平衡。究竟是什么操作?就是通过树旋转操作。
树旋转操作有四种情况:
- LL型
先来张图体会一下: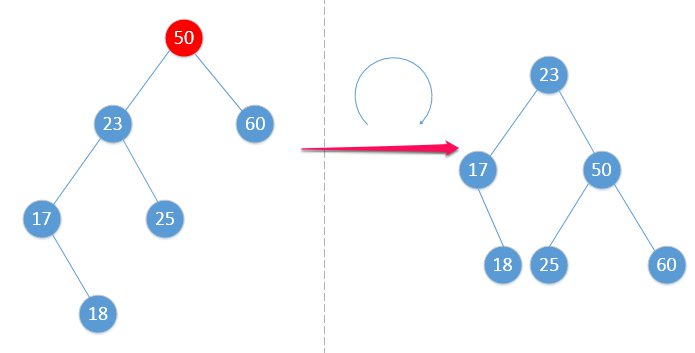 avl-2
avl-2
可以看到,50的平衡因子超过了1,不平衡,需要调整。这是什么类型?这是在不平衡节点的左子树的左子树上发生的事情。所以,它是LL型。
结合上图说明,它要做的工作有两步:
- 以50的左孩子23为中心,右旋转;
- 23的右子树被移动当作50的左子树(无右子树情况下,无需这一步)
- RR型
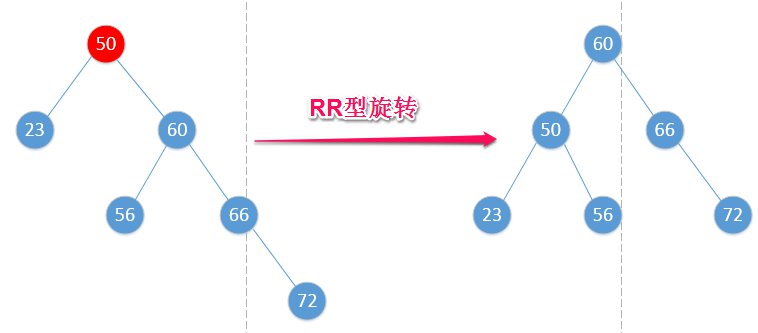
同理地,RR型旋转要做的工作:
- 以50的右孩子60为中心,左旋转;
- 60的左子树被移动当作50的右子树(无左子树情况下,无需这一步)
LL型和RR型都还算是比较简单的。后面来俩复杂点的,先看图:
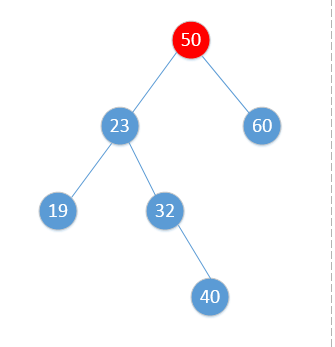
这怎么搞?如果你直接右旋转的话,你会发现将不符合排序树的性质,因为32比23大了。为什么会这样呢,因为32是23的右子树啊。这事情发生在不平衡节点的左子树的右子树上,所以它叫LR型。
- LR型
接着上面的图说明,要解决LR型的旋转还是有点套路的,如果把50的左子树变形成LL型那样的就好了。是,就这样做。
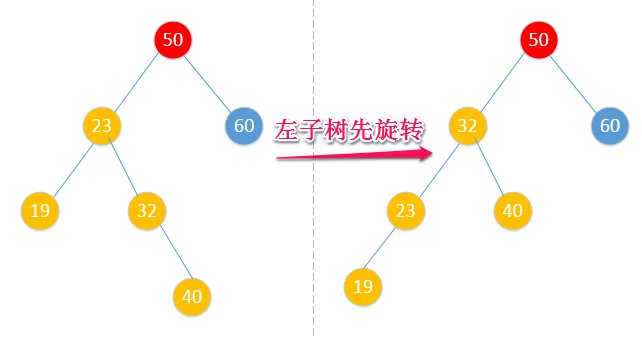
先解决左子树姿势不正确的问题,然后你发现可以直接右旋了。
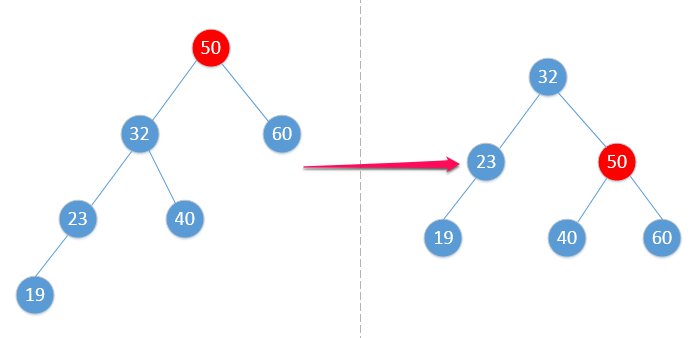
- RL型
看懂了LR型,再来看RL型,那就是如法炮制了。
先解决右子树姿势问题,再左旋。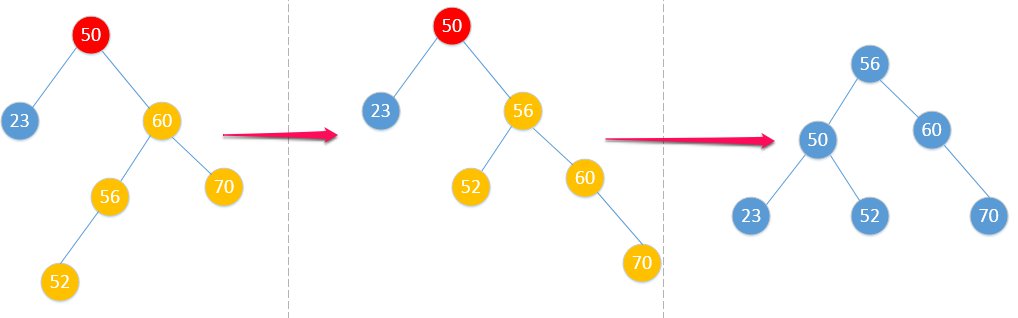
知道怎么解决平衡了。还有一个困扰的问题是,如何检测不平衡的发生,这个事情发生在插入节点甚至删除节点的时候。事实上只需检测不平衡的最小子树就行了,因为不平衡是建立在已平衡基础上的。所以只需要向上查找不平衡的节点就可以了。
上面的二叉排序树还派的上用场,先改造一下:
有了上面的函数,我们就可以根据是否平衡来进行树旋转操作了。(朋友们有没有更好的判断平衡的方法?)
下面实现四种插入的情况:
|
|
这样,四种类型的旋转也完成了(在码这四种操作的时候头有点晕=。=),好像差不多了。但事实还有一步,就是如何知道不平衡时采用哪种旋转,我看了很多博客,几乎都没有提到这一点。也许是觉得太简单了,略过了=。=
所以,在这里再分析一下旋转类型的判断,具体看代码注释:
|
|
实力分析一波:
只有在插入和删除的时候,才会出现不平衡。一切都建立在二叉查找树的插入和删除操作上。
- 插入
插入的时候,因为整棵树事先是平衡的,所以只需要往上查找不平衡的节点就行,然后根据类型执行旋转操作。
插入还好,最多也就两次旋转。因为插入的时候,只根据某一个节点进行调整。
- 删除
删除就不一样了,先按照普通的BST进行删除,而这个时候就需要进行平衡检查,怎么个检查法?插入的时候,好歹节点是插进来的,可以根据它往上查找,但删除节点后,节点都不存在了,怎么检查呢?
可以明确的一点是:
假如一个节点被删除,那替代它之后的节点以及往上的父啊祖啊什么的节点,平衡因子都可能发生变化。
“嘿嘿,难道不是像插入那样,找到第一个不平衡的然后调整完不就得了?”
其实,你在找到第一个不平衡的节点调整完之后,只是局部调整好了。来张图你就懂了: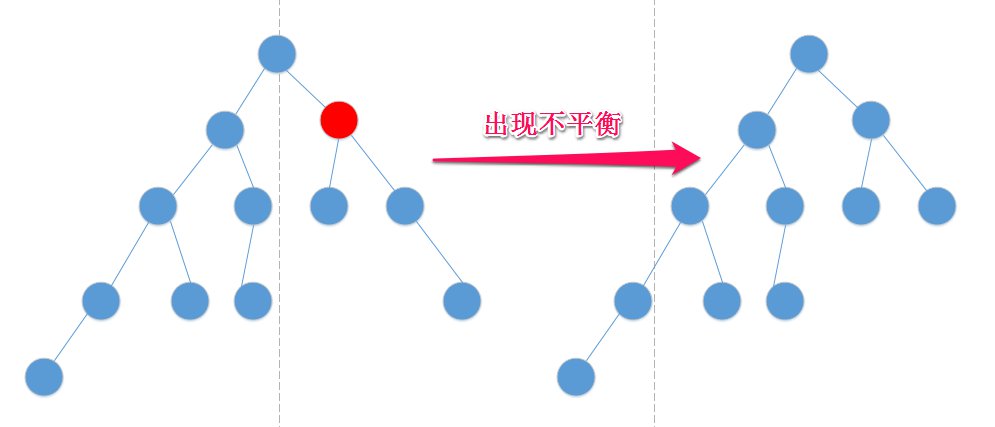
然后你调整完之后,变成了这样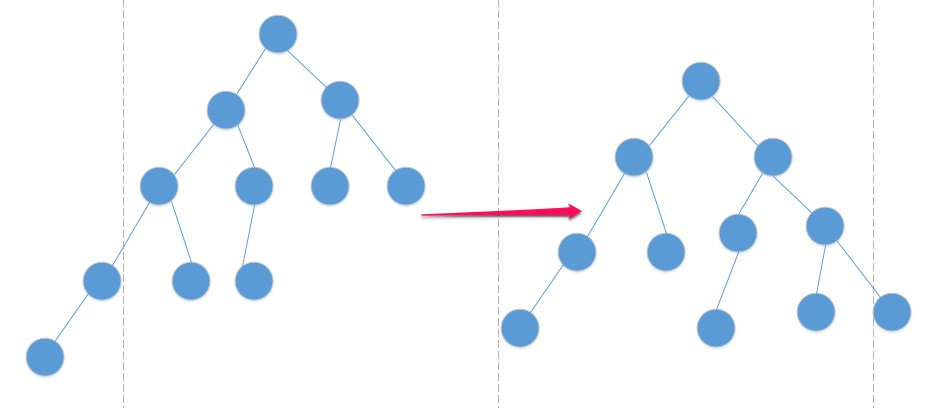
“本来就应该这样,这不很好吗?”
但是你发现这所谓局部的子树,高度已经发生了变化,由5变成了4。
你想一下,要是它的爸爸的另一个孩子,也就是它兄弟那边,高度是6(按照定义符合AVL树),造成了爸爸的平衡因子超过2,这可咋整?然后你又要调。
更糟糕的是,调完后又发现爷爷又不平衡了,所以继续。。。如此,直到根节点(这是最坏情况)。
所以,删除对于AVL树来说是一个糟心的过程。而且,删除一个节点很容易就造成整棵树的不平衡,造成调整多次。
由此,在原来BST的基础上,添加调整平衡的代码:
|
|
|
|
终于把AVL树一步一步给实现了,长舒一口气。感觉AVL树已经让你很疲倦了,但是,红黑树还没有开始。
为什么要有红黑树?AVL树跟红黑树比差哪了?
刚才在AVL树中,已经看到AVL树的删除操作在最坏情况下,调整的次数是O(logn)
AVL树在红黑树面前,几乎就是小巫见大巫,做好心理准备吧,见识见识这真正变态级的数据结构:
再遇红黑树
就像练了级回来再次挑战一样,我想这次已经有了足够了的资本。
红黑树的性质
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
红黑树为什么变态?
因为你就算埋头看个几天,甚至都没搞清楚它,即使你记下了步骤,依然不知所以。看红黑树,就是硬着头皮看的。
所以,为了避免懵逼。还是先入手一下2-3树或者2-3-4树。
“怎么还不讲红黑树,之前就已经绕过一次了,这是要干嘛?”
没办法,直接讲红黑树,就算看懂了,很快就忘了,因为你根本不知道它的意义。它究竟为谁而生?
2-3Tree
2-3树对于人类思维来讲非常好理解(表骗我)。你先别问2-3树的好处是啥,它在我这里,只是理解红黑树的一个工具。
注意,它不是二叉树了,但它是二叉排序树的一种泛化版。它由2-节点跟3-节点构成。
- 定义:
- 要么空,要么就是这样:
- 对于2-node,它有一个键值key,和两个子节点(左、右)。左节点是一个2-3节点,它里面的元素都比key要小;右节点也是一个2-3节点,它里面的元素都比key要大。
- 对于3-node,它有两个键值A和B,以及三个子节点(左、中、右)。左节点是一个2-3节点,它的元素比A都要小;中节点是一个2-3节点,它的元素的值介于A和B之间;右节点也是一个2-3节点,它的元素比B都要大。
叶节点的孩子节点为空(null links)。
直接上《算法》里的图: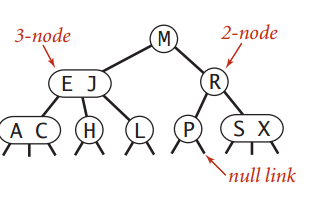
一颗完美的2-3树,它到所有null links的距离都是一样的。
诶,我们要讲就要讲完美的,其他的不谈。
2-3Tree查找
查找就不用说了吧?跟BST是一个道理,从祖宗开始往下查,有则有,无则无。
《算法》里的图很形象: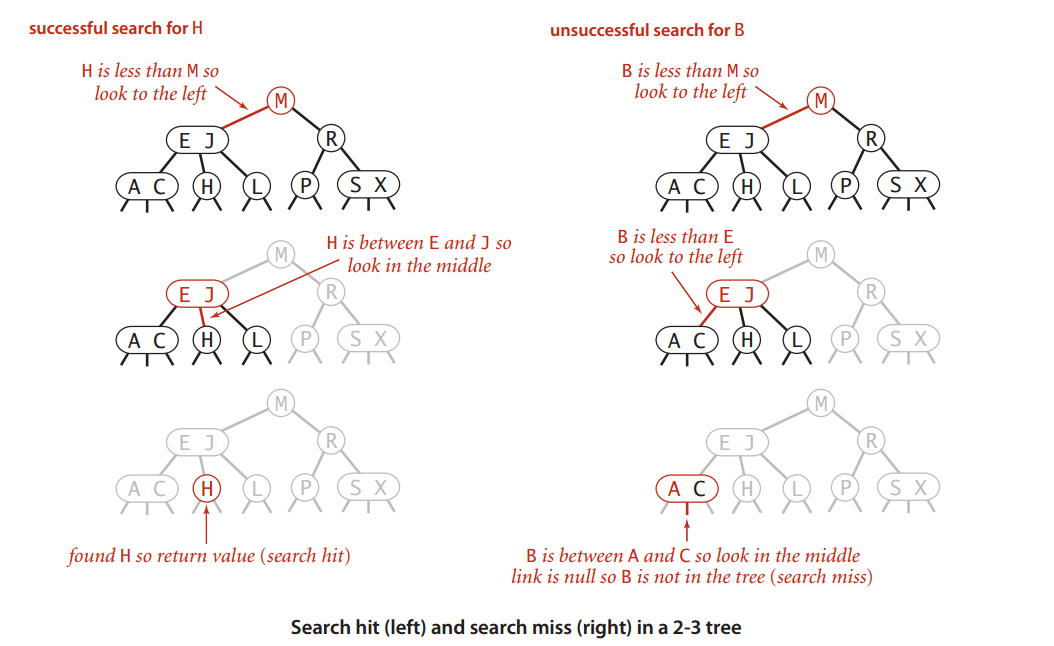
2-3Tree插入
套路都差不多了,插入都是基于查找。
- 往2-node里插
如果插入一个节点时,查询刚好终止于一个2-node,那么很幸运,这个很好操作,只需要将这个2-node变成一个3-node即可:
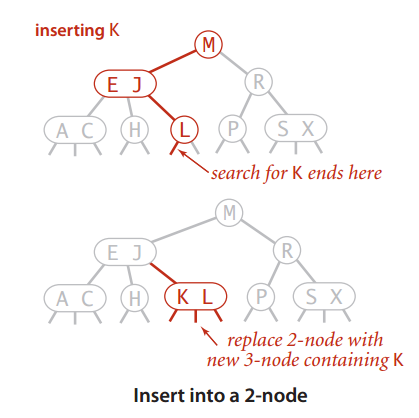
- 往3-node里插
但是往3-node里面插入节点就没那么友好了,可以说,相当复杂:
- 插入的3-node是一个由独立的3-node所构成的树
这个还相对简单点,先把它变成一个暂时的4-node:
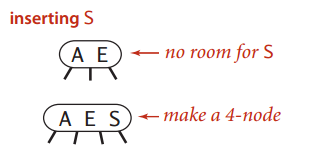
然后分割这个4-node,中间那个推上去,把这个4-node变成一颗2-3树: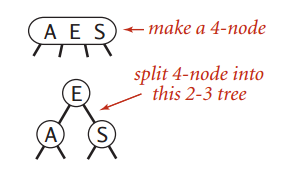
- 插入的3-node的父节点是一个2-node
第一步,还是先把它变成一个暂时的4-node:
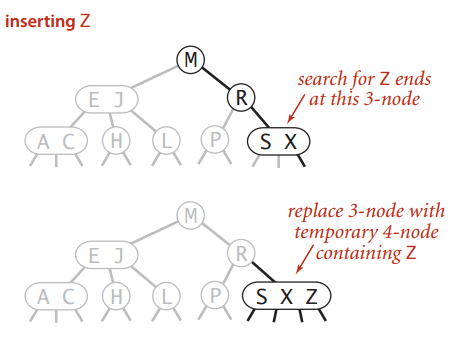
然后,分割这个4-node,把中间那个推上去: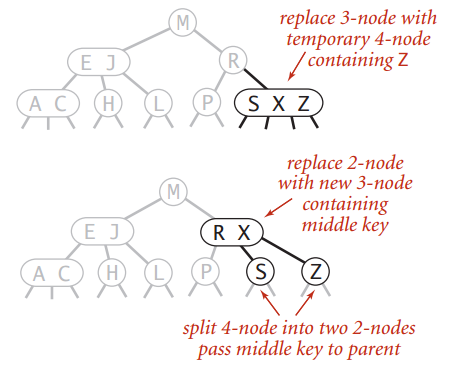
- 插入的3-node的父节点是一个3-node
第一步,把它变成一个4-node: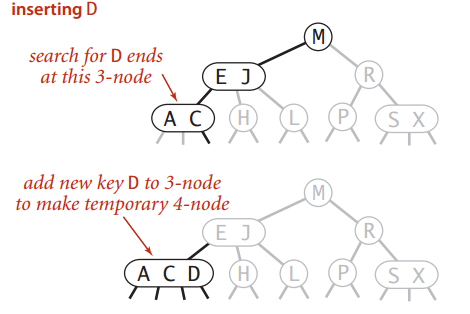
然后,分割,推中: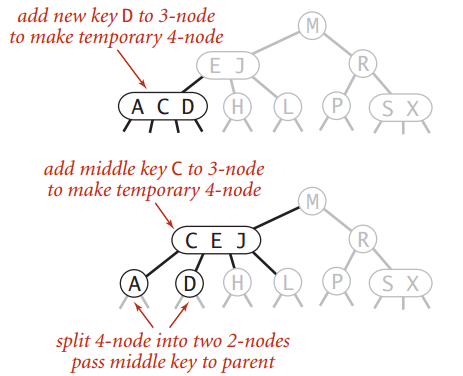
然后你发现,这一推,父节点也变成4-node了。咋办?那就继续推中:
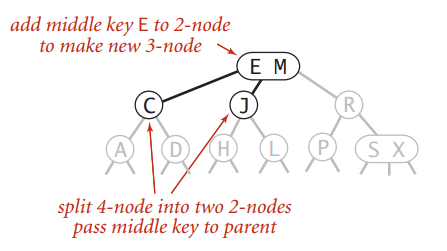
- 根节点是4-node
推中推的很爽,结果发现王座变成了4-node。其实这个跟上种情况一样,继续推中,推出一个新的根节点:
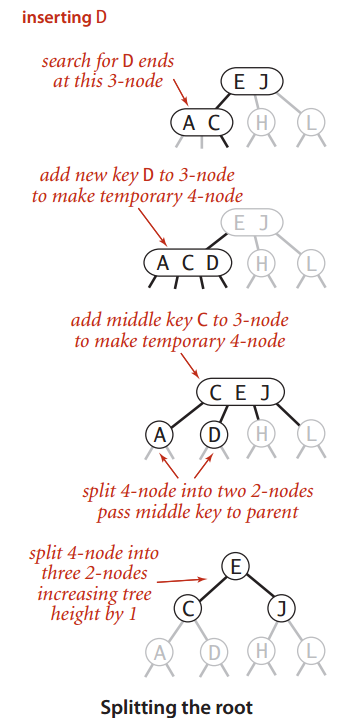
所以,在插入元素到3-node的时候,暂时生成的4-node“推中”是一个有讲究的操作。总结一下“推中”到底能遇上哪些情况:
根节点“推中”
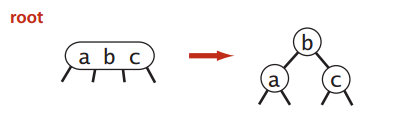 2-3_tree-12
2-3_tree-12“推中”的对象是2-node
有两种情况:
- 4-node是2-node的左子树,这个推到2-node左边;
- 4-node是2-node的右子树,这个推到2-node右边;
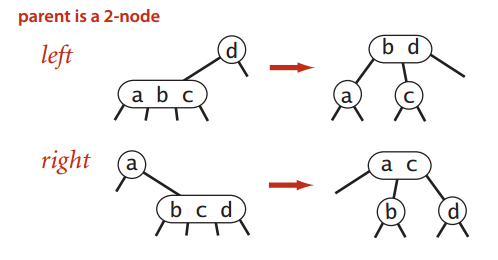
- “推中”的对象是3-node
有三种情况:
- 4-node是3-node的左子树,这个推到3-node左边;
- 4-node是3-node的中子树,这个推到3-node中间;
- 4-node是3-node的右子树,这个推到3-node右边;
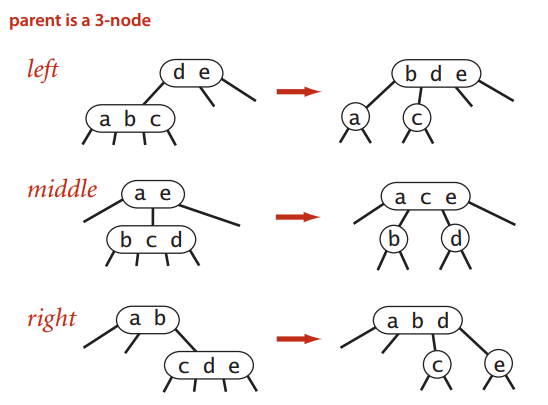
看完上面的东西,有什么值得注意的吗?
可以知道,2-3树在单纯插入的时候高度是不会变的,变是变在“推中”的操作上。而且,它时刻都在保持着完美平衡。因为它完美平衡,所以插入操作始终发生在底部。
完美平衡的好处之一就是查找快。这不用说了吧?
“AVL也快啊~~”
是,我之前说什么来着,AVL它删除可能会很耗时,旋转太多!2-3树一看上去都不用旋转,是不是6翻了?
那好吧,就来实现实现。
根据以上的规则,可以写出一堆代码出来,它对代码实现不是很友好。你可能觉得挺简单的,但事实上,涉及到了两种节点,在考虑情况的时候就很头疼。能不能只靠一种节点来实现,不要这些什么2-节点、3-节点,甚至4-节点的,写出来就感觉麻烦。
2-3树到红黑树
终于到了红黑树了,这次不会再绕弯了。
其实,看完这些,估计心里就有些想法了,红黑树该不会是2-3树进化过来的吧?
呃,这谈不上是进化,只能说红黑树是单纯的二叉树实现了2-3树。
“逗我呢,这哪是二叉?那开三叉的3-节点怎么搞?”
对,我要说的就是3-节点要怎么搞,我们要对3-节点进行一下处理,《算法》书上说叫对3-节点进行编码。
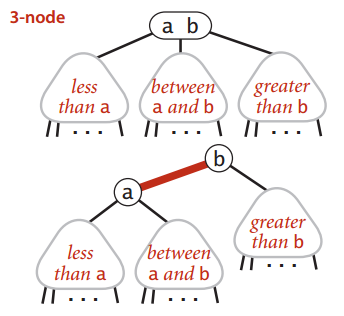
如同书上所说,一个3-node,它变成了两个2-node。之前的3-node的左元素被抽离出来,变成了3-node的右元素的左节点。并且这两个2-node由红线相连。把2-3树里的所有3-node都变成这样,就成了一个红黑树的雏形。为什么只是雏形?因为描述边的特点没有描述节点来的方便。我们加点料看看。
理解刚才那句“3-node的左元素被抽离出来,变成了3-node的右元素的左节点”是很重要的。根据书上描述,这里要定义3-node的右元素为h节点:
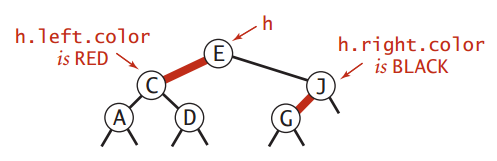
并且,还有两件重要的事,直接说明了红、黑节点究竟是怎么着色的:
- h节点的左节点为红节点;
- h节点的右节点为黑节点;
此外,空链接根据约定,也为黑节点。
怎么样?总算知道了吧?红黑树的红与黑不是在变戏法(有些同志像介绍戏法一样介绍红黑树,怎么看得懂?),它只是约定俗成而已。
再来看看红黑树的五条性质:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
1、3都不必说了(第二条性质待会儿再说)。其实,有些人好奇就好奇在为什么有4、5这样的性质。现在,就给你分析一波:
为啥不能有两个连续的红色节点?
如刚才的图,h节点是3-节点的右元素,只有3-节点的左元素才有变成红节点的条件;如果h节点也想变红,除非它还有个兄弟在它右边,但是如果它还有右兄弟的话,那这个节点就不是3-节点,而是4-节点了(注意这里的描述,h节点不是不可以变红,只是它暂时会变红,就跟2-3树里会有临时的4-node一样)。为啥所有路径上的黑色节点数量一样?
先想一下2-3树,它到所有叶节点的距离都是一样的。再想想红节点是怎么出来的?红节点是3-节点的左元素分离出来的,并且用红线跟h节点相连。对于2-3树来说,红线是不是多余的东西?剩下的自然就都是黑线了啊,红线和红节点在2-3树这个层面上来说,影响不到2-3树的高度。可能说的有点不明白,那下图绝对能让你明白:
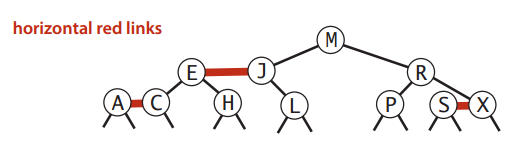
那么接下来,就是红黑树的神级操作。唯一会让你困扰的是,红黑树在处理插入3-node(相对于等价的2-3树)的时候,不是采取“推中”的策略,而是“分裂”的策略(从这里的理解开始,我跟《算法》里的描述可能有些许不一样,但总归来讲思想还是一样的)。
我要引导的是,如何从2-3树的概念里转换过来:
依然像2-3树那样进行插入操作。所以,在下面的描述里,关于2-node,3-node,4-node这些,只是红黑树里等价于对应2-3树的说法。
树旋转操作
介绍红黑树的插入之前,我想先介绍一下树旋转。但是为了更好地理解,先来个插入操作作为引子。
往独立的2-node里面插(只有root节点)
2-3树的2-node:
红黑树的2-node:
- 插入一个相对于b小的元素a:
2-3树: rbt-6
rbt-6
红黑树: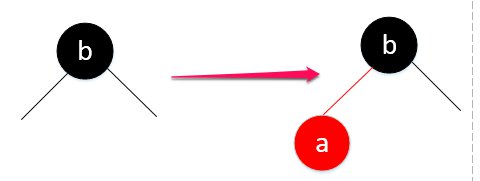
这一步,显然,对照一下2-3树,2-3树的2-node变成了3-node,而3-node显然要编码成红黑树的标准。b成为所谓的h节点,a作为它的左节点,当然也就是红线相连,并且a节点标成红色。
- 插入一个相对于b大的元素c:
2-3树: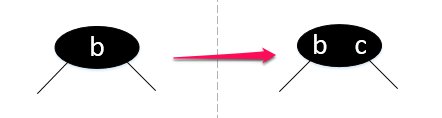 rbt-8
rbt-8
红黑树: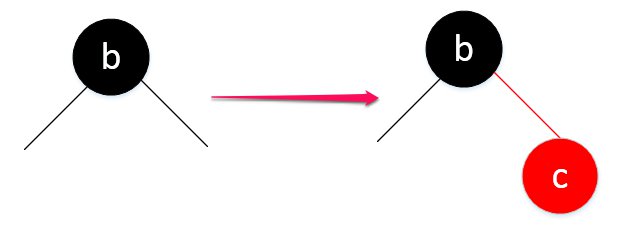
“嘿嘿嘿,你怎么乱搞?”
这不是乱搞,首先,我们得按照二叉排序树的规定来插入节点。
“插入就插入,为啥把它搞成红的?不是说只有左元素才有这个条件吗?”
红的是因为要符合红黑树的第五条性质。
“那不矛盾了?”
先别急,我还得旋转它呢: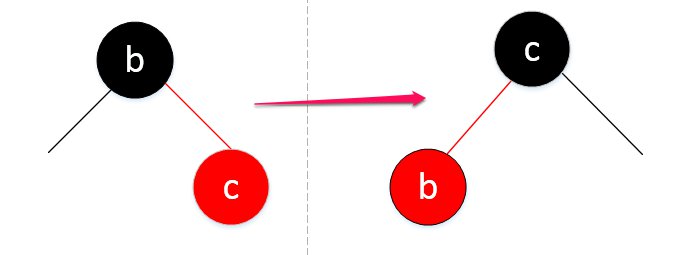
明确一点,红黑树的插入操作还是按照二叉排序树的套路来(不然之前复习过的都白费了不是吗=。=),默认插入的节点是红节点。产生冲突了(和红黑树定义违背)再进行树旋转和变色操作。
上面的例子里,就出现了需要调整的情况,《算法》上总结了两种旋转操作:
- 左旋转
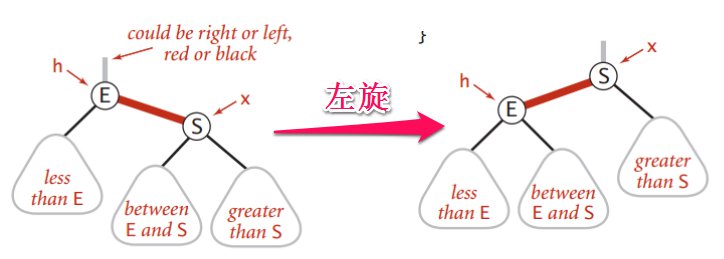 rbt-11
rbt-11
- 右旋转
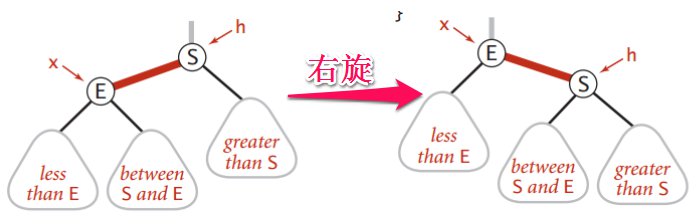 rbt-12
rbt-12
“为什么还会有右旋转?(对啊,我也想问)。这不是把本来正确的给整成错的了吗?”
- 变色
呵呵,上面我已经说过,那个所谓的h节点不是不可以变红,当它是4-node的中间节点是,它会是红的,所以这个右旋转其实是起到一个过渡作用,看下面的情况: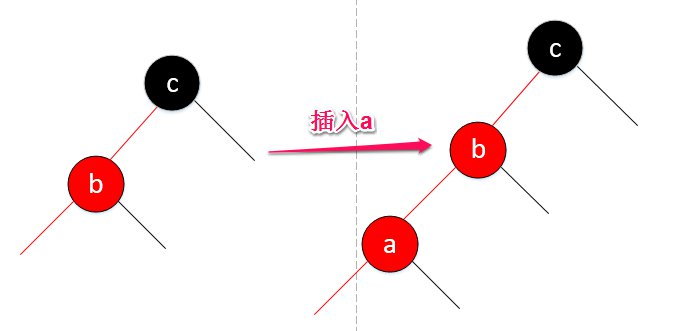 rbt-13
rbt-13
你看,我想插入a(b已经红了),那它就得在b左边,形成一个临时的4-node,而对于临时的4-node,是需要“推中”的,在红黑树里,其实就是LL旋转(b为中心):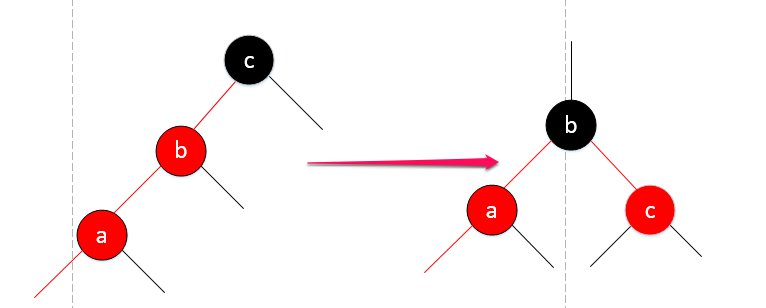
“这下左右都是红的了,还搞毛。。。”
忘了4-node怎么拆分的了吗?,把b节点推上去,4-node变成3个2-node,放在红黑树的概念里,自然也就没有所谓的红节点了: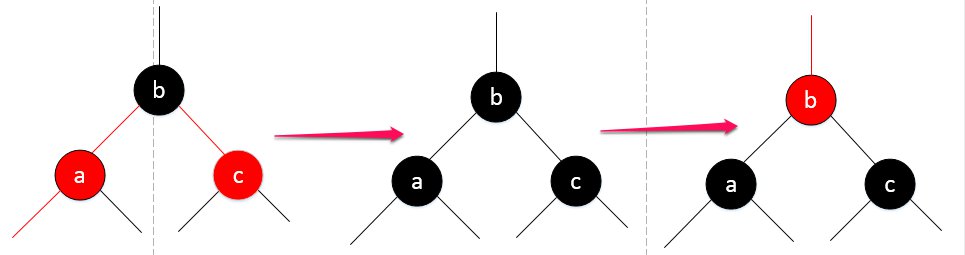
注意图中的最后一步,我把b节点变红了。你应该可以理解,因为中间状态的时候,这个子树的黑色层级变高了,不符合红黑树的第五条性质。
但是,在b节点是根节点的情况下,不能变色,而且你即使翻转它的颜色,也是个多余动作。根节点是红或黑,都影响不到红黑树的第五条性质。而且,你可以想一下,根节点如果设成红色,就没法往下进行了。所以,保持根节点是黑色的。这也就是红黑树为什么有第二条性质。
“b不是根节点的话,如果b节点本身是左边的子节点还好,如果是右边的子节点,又得左旋转。”
嗯,是的。这里的插入操作,有时候需要多次旋转,最多三次旋转。
至于这些旋转操作,前面已经介绍过AVL树的旋转操作,所以这里不再重复介绍(就多了根红线嘛。。看前面的LL、LR、RR、RL去)
插入操作
上面已经提到过一种插入操作,下面继续,要知道,红黑树的插入除了发生在根节点,就是在叶节点了。
往底部的2-node插入
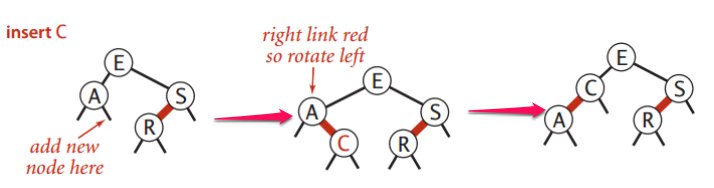
和在根节点插入差不多,只不过有父节点存在而已。
下面,往3-node里面插入,和2-3树一样,很多种情况:
一个单独的3-node
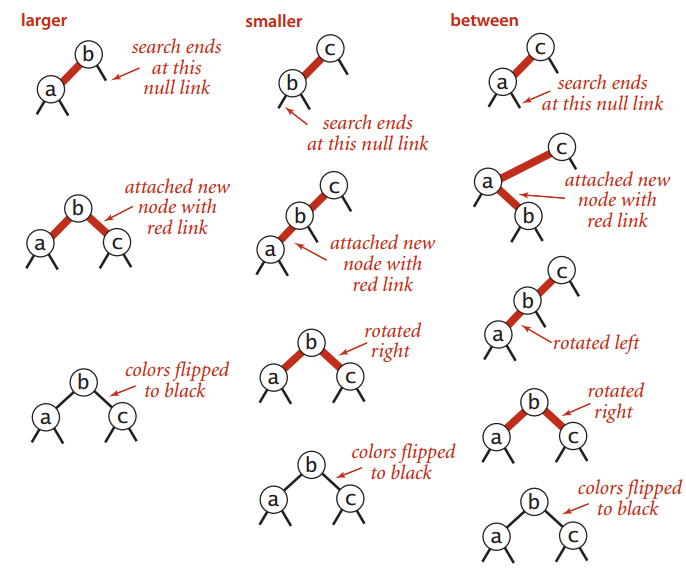
往底部的3-node插入
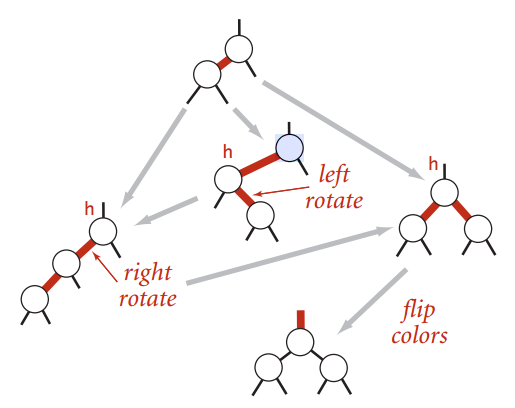
有时候旋转最多要三次,就是如下这种情况(为啥不是两次?两次也是对的,马上就讲):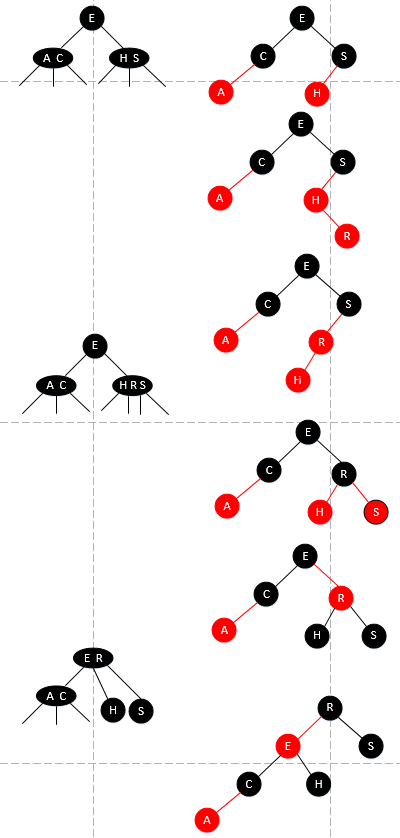
好了,我算是把《算法》上的2-3树到红黑树基本复述了一遍。
“诶,貌似没讲完,还有删除操作呢?”
先打断一下,你可能会发现,2-3树概念里的红黑树,虽然处处符合红黑树的5条性质,但总感觉不够。而且你如果之前看过其他的博客,你会发现跟大多数讲的不一样,你肯定会提出质疑:
上面实现的红黑树,如果节点没有左子树,往右边插入,就一定会调整到左边,因为它不符合所谓的red link(2-3树)定义。但事实上,红节点在右边又怎么了?没毛病啊,根本不会违背红黑树的性质。红色节点通通都是左节点,强行右转左的操作让你很不爽。
所以,你觉得这可能是劣化版的红黑树。
我当然知道你在想什么,2-3-4树,对不对?是的,2-3-4树才是红黑树的对应版本,为什么不早点说?其实本质是一样的,所以,这里就是个玄学问题(笑)。区别在4-node,看下图: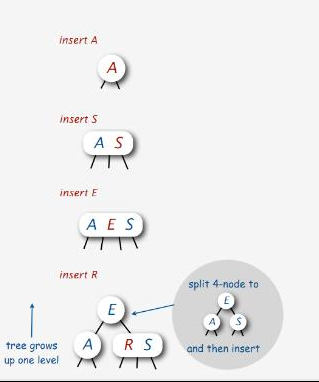
关键是你怎么看待4-node,2-3树里也会有4-node,只不过它是暂时存在的,“推中”是它的核心操作;对于2-3-4树来说,又是怎样一副景象呢?在遇上4-node的时候,难道还要生成一个临时的5-node吗?并不是,在这个时候,它需要先“分裂”成3个2-node(其实就是2-3树的“推中”)。所以,一切取决于你是选择他“推中”还是“分裂”,英文原话叫“bottom-up 2-3”跟“top-down 2-3-4”。
事实上,我讲的这个版本的红黑树,它不是劣化版本,反而更加高级。它是红黑树的发明人之一Robert Sedgewick先生为了减少原有红黑树插入/删除需要处理的情况数量,自己改进的算法,它叫Left-leaning red-black trees(LLRBT),即左偏红黑树。在它的世界里,红节点就是要左倾的。它比起一般的RBT,有以下优点:
- 它可以与2-3-4树保持完美的一一对应
- 它可以保持完美的黑链平衡
我在这里稍微提一提2-3-4树吧,2-3-4树允许树中有这样的节点:
- 2-node:一个key,2个孩子
- 3-node:两个key,3个孩子
- 4-node:三个key,4个孩子
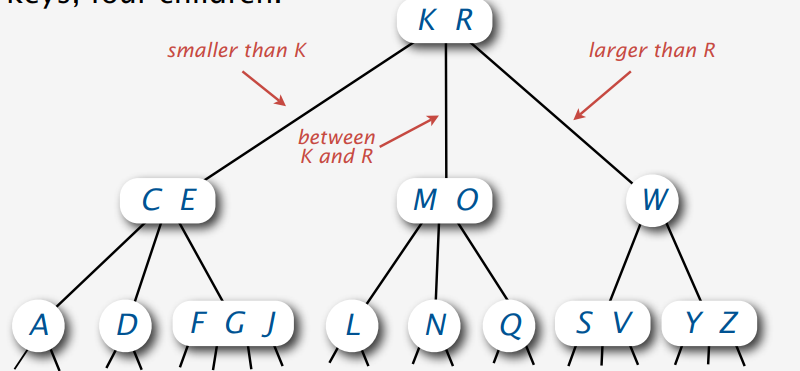 rbt-21
rbt-21
普通RBT编码方式:
3-node的编码方式跟刚才不一样了,红线可以在左,可以在右。4-node作为合法存在,它的两个子节点都可为红。
LLRBT编码方式:
3-node的编码方式就是我上面讲的,它不允许红节点存在于右边。而关于4-node,你可以看上面讲的变色操作。所以,你明白了,我其实一直在讲的就是这个LLRBT。
删除操作
插入都这么艰难了,删除岂不更加费脑?红黑树的删除包含哪几种情况呢?我不会去分析那些什么父黑叔红,父红叔红各种情况的,那样只会让人眼花缭乱。明明都讲了2-3树,还要各种记红啊黑什么的,那我讲2-3树有何用?
在LLRBT里,删除一个节点,比插入还简单,我在这里提供一个策略:
- 找到被删节点的后继节点
- 后继节点的key替换被删节点的key
- 删除后继节点
套路听上去跟普通的BST差不多,没错,就是一样,删一个节点,就是找到后继节点,把key替换掉,然后删掉后继节点。只不过你要进行变色而已。晕~~
明确一点,删除一个红节点不会影响到红黑树的性质。不是吗?
“那我删的后继节点就是黑的怎么办?”
“把它变成红的。”
黑的是啥?黑的在2-3树里就是2-node,普通节点。红的是啥?红的存在于2-3树里的3-node,也可以暂时存在于4-node。如果我删的是黑节点,也就是2-node,那我就要想办法把它变成4-node来进行删除。
“WTF?黑的变红的很容易啊,三个黑的组一块,变成一个4-node不就完了?”
是啊,我就是要利用临时的4-node。不过,你还需要考虑,你是从别的层级借过来黑节点,这意味着,这颗子树的黑链长度遭到改变,有可能就破坏了整棵树的黑链平衡。我事先想强调的一点是,对于普通的红黑树,3-node的编码,左红或者右红都是没什么区别的,这一点影响不到红黑树的第五条性质。我们同样可以利用这一点。
“噢,那要怎么做?”
所以,意思就是利用同构的特点以及暂时的4-node对二叉树进行旋转加变色,但要始终保持黑链平衡。
先看图,之后再解释:
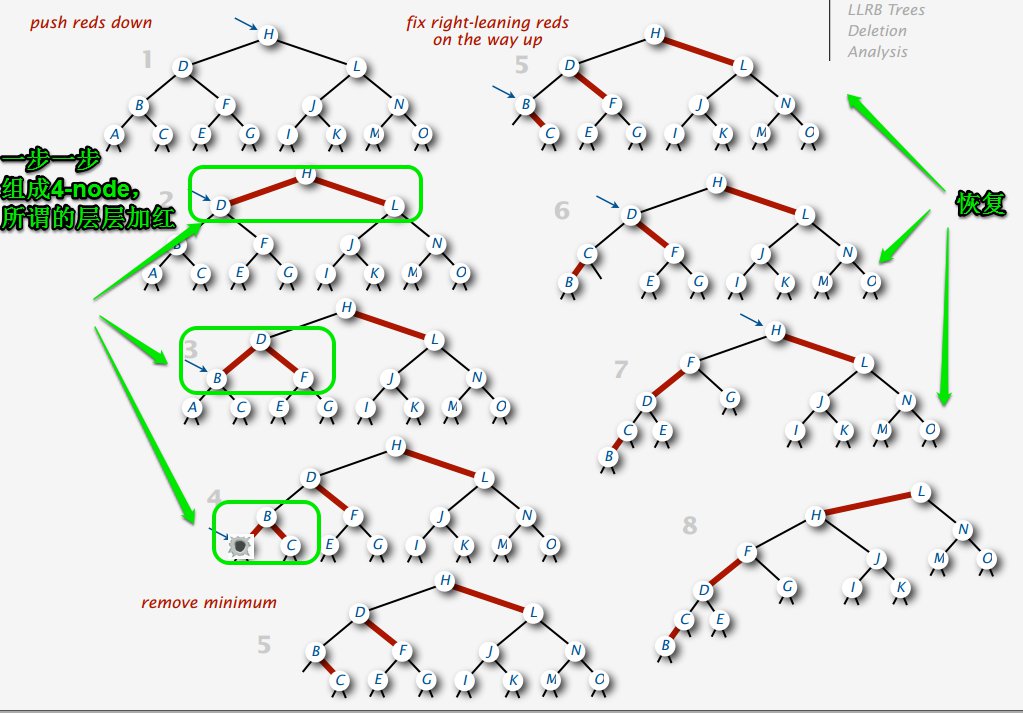
假如我要删掉这颗树(或者只是颗子树)的最小节点a,就从它的根节点开始往下逐层“加红”(其实就是利用暂时的4-node不断往下迁移),这样做是为了先保持黑链平衡,满足红黑树的第五条性质。等删掉之后,再通过旋转恢复成LLRBT的样子。
“哪有你这么理想,你这例子全是黑节点啊”
确实,情况还是有好几种的。
什么时候需要加红(变成临时的4-node)?在寻找后继节点的道路上,得分两种情况讨论。
先提个醒,在删除后继节点的时候,肯定是这种形态:
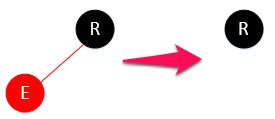
完美删除,丝毫不影响红黑树的性质。
查找路线在左子树
也就是查找时,判断在左子树,需要“左拐”。
- 情况一
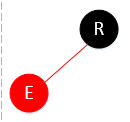
到达R节点时,因为查找的节点比R小,所以要左拐,但是看到E是红的,这种情况下,就不需要加红了嘛。直接往下走就行。
- 情况二
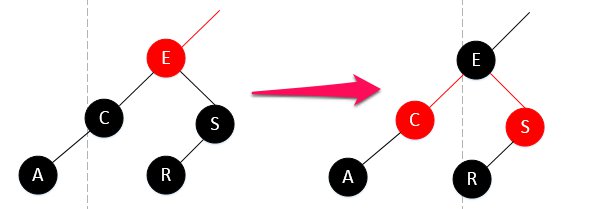
查找依然往左拐,但是看到C是黑的,如果此时直接对C动手,E的黑链就崩坏了,所以要它进行“加红”,公平起见,C和S都要变红。
- 情况三
情况三比情况二复杂点:
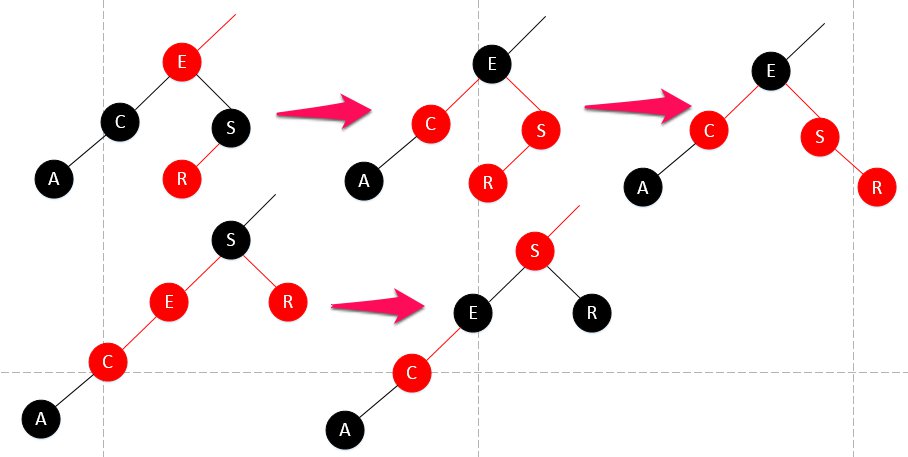
就是在给S变红时,S的左儿子是红的,这种情况跟插入时情况很像,只能旋转解决。
查找路线在右子树
可能拐着拐着,发现要往右子树拐了:
- 情况一

按照LLRBT的道理,右节点可能为红吗?反正先不管,先把R的两儿子都变红了再说。但偏偏遇上左节点已经红了,你说把右节点变红吧,黑链又崩坏了。所以就是这种情况,而且发生在根节点上,只需把它左红转换成右红,这样做依然不影响红黑树的性质。
- 情况二
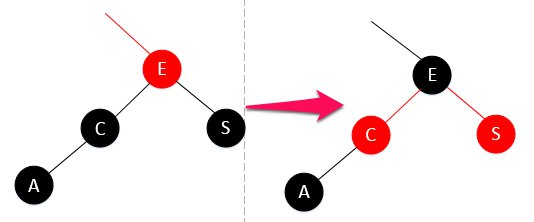
这种简单,直接变色就行。
- 情况三
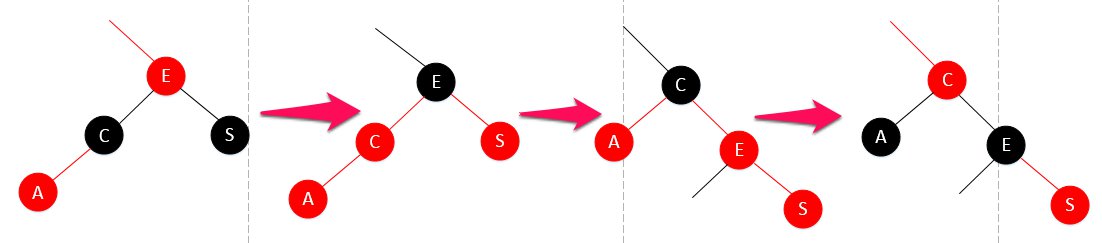
这种情况就是你发现当把E的左节点C变红了之后,C的左节点A居然是红的,这一变彻底违反红黑树性质,又得调,旋转,再变色。
总之,删除中所需要的临时形态就是这么多了,千万记住一点,临时操作虽说是临时,也不是LLRBT的形态,但也不能违背红黑树性质。失去了LLRBT的形态不要紧,只要你熟悉插入操作,那些什么右红变左红,4-node的“推中”,不是分分钟的事嘛。
最后,还是来份完整代码吧,也是根据《算法》的程序,写了个python版的:
|
|
可能想比一下AVL跟LLRBT的性能,那就pk一下,因为实现的有差异,可能不是很客观,仅供娱乐。
- 随机300个数据:
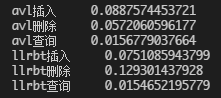 test-1
test-1
- 随机3000个数据:
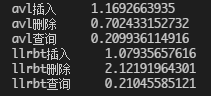 test-2
test-2
- 随机30000个数据:
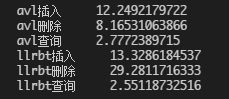 test-3
test-3
结果LLRBT竟然遭到无情暴击。。。看来还有待优化。到这里,有关红黑树的知识就介绍完了。
